La frazione (scuola media)

Video per chi non ama leggere: Matteo Ruffoni, 2023 frazioni, su YouTube, 22 marzo 2023.

tre quarti di orologio

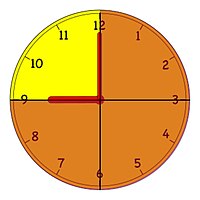
«Arrivo tra tre quarti d'ora» può capitare di sentirsi dire al telefono mentre si chiede ad un amico di raggiungerci. Con la quantità tre quarti si indica in modo preciso il tempo che si dovrà aspettare cioè 3 delle 4 parti, ogni parte è un quarto d'ora, in cui viene divisa l'ora. Una prima intuitiva definizione: una frazione, in questo caso ${\frac {3}{4}}$, permette quindi di esprimere una quantità non intera di una certa grandezza utilizzando una divisione seguita da una moltiplicazione.

Analizzando poi la frazione^VK a sé stante, cioè senza applicarla ad una grandezza, si può comprendere che la frazione si può interpretare come un numero^VK espresso attraverso una divisione, non eseguita, dalla quale eredita la proprietà invariantiva^VK.

Mappa per chi non ama leggere

Inserite il wiki, la lingua e il titolo della pagina

Terminologia

Se la frazione è ${\frac {3}{7}}$, $3$ rappresenta il numeratore, $7$ il denominatore e la barra la linea di frazione.

• Numeratore: indica le parti considerate
• Linea di frazione: indica la divisione
• Denominatore: indica il numero di parti congruenti, uguali, in cui è diviso l'intero.

Tipi di frazione

Ci sono diversi tipi di frazioni:

• Propria:se il numeratore è < del denominatore.
• Impropria:se il numeratore è > del denominatore.
• Apparente:se il numeratore è multiplo o uguale al denominatore.
• Unitaria:se il numeratore è = a 1.
• Decimale:se il denominatore è una potenza di 10.
• Diadica:se il numeratore è una potenza di 2.

Fare la frazione di un numero

Indicare con tre quarti ${\frac {3}{4}}$ d'ora 45 minuti è comune. Partendo da questo esempio possiamo provare a capire come si deve procedere per calcolare il valore corrispondente ad una frazione di una quantità.

tre quarti di orologio

Facendo riferimento alla figura si comprende che un quarto di ora ${\frac {1}{4}}$ corrisponde a 15 minuti e quindi moltiplicando per 3 si ottengono i ${\frac {3}{4}}$ d'ora corrispondenti a 45 minuti.

Dall'esempio ricaviamo la regola generale:

il numero corrispondente alla frazione di una determinata quantità si calcola dividendo la quantità per il denominatore e moltiplicando il risultato per il numeratore

Ad esempio:

i due di terzi di 96 corrispondono a 64 infatti

$96:3=32\ e\ 32\cdot 2=64$

Esercizi per capire la frazione di un numero

Punto aggiunto per ogni risposta corretta:
Punti sottratti per ogni risposta non corretta:
Ignora i coefficienti di domanda:

1 ${\frac {1}{4}}$ di 12 corrisponde a ?

	$3$
	$4$
	$6$

2 Calcola i ${\frac {3}{5}}$ di 35

	$21$
	$3$
	$15$

3 Calcola i ${\frac {7}{6}}$ di 24

	$21$
	$3$
	$28$

4 ${\frac {2}{15}}$ degli alunni della classe, 30 allievi, ha risultati brillanti in matematica, quanti sono?

	$4$
	$15$
	$2$

5 Uno sconto del 20% corrisponde alla frazione ${\frac {20}{100}}$, le scarpe costano 120€ a prezzo pieno a quanti euro corrisponde lo sconto?

	$20$
	$24$
	$12$

Esercizi per imparare a calcolare la frazione di un numero

• Coding con scratch frazione di un numero

Altri tipi di frazioni

Numeri misti

Il numero misto è l'addizione di un numero naturale e di una frazione propria. Tutte le frazioni improprie possono essere riscritte sotto forma di numeri misti.
Es: ${\frac {11}{4}}={\frac {4}{4}}+{\frac {4}{4}}+{\frac {3}{4}}=1+1+{\frac {3}{4}}=2+{\frac {3}{4}}$.

Frazione complementare

La frazione complementare è la frazione che permette di completare l'intero
Es: ${\frac {11}{4}}+{\frac {1}{4}}={\frac {12}{4}}=3$.

Frazioni equivalenti

Le frazioni equivalenti sono quelle frazioni che hanno numeratore e denominatore diversi, ma danno lo stesso rapporto. Per trovare una frazione equivalente bisogna trovare il numeratore e il denominatore.
Es:${\frac {1}{2}}={\frac {2}{4}}$ perché ho eseguito i seguenti passaggi: 1 x 2 e 2 x 2, cioè ho moltiplicato numeratore e denominatore per uno stesso numero.

Casi particolari

• Tutte le frazioni con denominatore uguale a 1 sono apparenti e corrispondono ad interi.
• Se il denominatore è uguale a 0, la frazione non rappresenta una quantità.
• Se il numeratore è uguale a 0, la frazione risulterà 0.
• Se sia il numeratore che il denominatore sono uguali a 0, la frazione risulterà indeterminata.

Operazioni con le frazioni

Alle operazioni con le frazioni è dedicata una lezione intera, che in breve è riportata qui sotto.

Addizioni e sottrazioni

-Se hanno lo stesso denominatore Per sommare o sottrarre delle frazioni con lo stesso denominatore bisogna mantenere lo stesso denominatore e sommare o sottrarre i numeratori delle singole frazioni.

Es:

• ${\frac {7}{14}}+{\frac {21}{14}}={\frac {28}{14}}={\frac {2}{1}}=2$
• ${\frac {49}{42}}-{\frac {35}{42}}={\frac {14}{42}}={\frac {1}{3}}$

-Se le frazioni hanno denominatore diverso

Video per chi non ama leggere: Matteo Ruffoni, Frazioni addizione, su YouTube, 13 mag 2018.

Per sommare o sottrarre delle frazioni con denominatore diverso devo:

1. Trovare l’m.c.m dei denominatori delle frazioni;
2. Trovare le frazioni equivalenti che abbiano come denominatore l’m.c.m;
3. Sommare o sottrarre le frazioni.

Es:

• ${\frac {1}{3}}+{\frac {7}{2}}={\frac {2+21}{6}}={\frac {23}{6}},m.c.m(3;2)=6$

Moltiplicazioni

Video per chi non ama leggere: Matteo Ruffoni, Moltiplicazione naturali frazioni, su YouTube, 6 mag 2018.

Per moltiplicare delle frazioni posso usare due metodi:

Video per chi non ama leggere: Matteo Ruffoni, Moltiplicazione di frazioni 2, su YouTube, 15 mag 2018.

1° modo)

${\frac {1}{3}}\cdot {\frac {1}{3}}={\frac {1\cdot 4}{3\cdot 5}}={\frac {4}{15}}$

Per moltiplicare due frazioni fra loro devo moltiplicare i numeratori e i denominatori e ridurre il risultato ai minimi termini.

2°modo) Semplificazione incrociata

${\frac {8}{3}}\cdot {\frac {9}{10}}={\frac {{\bcancel {8}}^{4}}{{\bcancel {3}}_{1}}}\cdot {\frac {{\bcancel {9}}^{3}}{{\bcancel {10}}_{5}}}={\frac {4\cdot 3}{1\cdot 5}}={\frac {12}{5}}$

(semplifico il 3 con il 9 e l'8 con il 10)

Frazione reciproca (o inversa)

Ogni frazione ha una sua reciproca, o inversa, cioè un'altra frazione che moltiplicata con la prima da come risultato 1. Ad esempio:

${\frac {7}{8}}\cdot {\frac {8}{7}}={\frac {{\bcancel {7}}^{1}}{{\bcancel {8}}_{1}}}\cdot {\frac {{\bcancel {8}}^{1}}{{\bcancel {7}}_{1}}}={\frac {1\cdot 1}{1\cdot 1}}={\frac {1}{1}}=1$

Ed anche:

${\frac {1}{2}}\cdot 2={\frac {1}{{\bcancel {2}}_{1}}}\cdot {\bcancel {2}}^{1}=1$

Qui sotto una tabella con alcune frazioni e la loro reciproca

Frazione	Reciproca
${\frac {2}{3}}$	${\frac {3}{2}}$
${\frac {5}{4}}$	${\frac {4}{5}}$
${\frac {1}{2}}$	$2$
$3$	${\frac {1}{3}}$
$1$	$1$
$0$	non esiste

Divisioni

Video per chi non ama leggere: Matteo Ruffoni, Frazioni divisione, su YouTube, 16 mag 2018.

Per dividere due frazioni bisogna invertire la seconda frazione e moltiplicarla per la prima.

Es:

${\frac {1}{6}}:{\frac {1}{3}}={\frac {1}{6}}\cdot 3$

Ora basta semplicemente moltiplicare le frazioni.

${\frac {1}{6}}\cdot 3={\frac {1}{{\bcancel {6}}_{2}}}\cdot {\bcancel {3}}^{1}={\frac {1}{2}}$

${\frac {3}{7}}:{\frac {6}{5}}={\frac {3}{7}}\cdot {\frac {5}{6}}={\frac {{\bcancel {3}}^{1}}{7}}\cdot {\frac {5}{{\bcancel {6}}_{2}}}={\frac {1\cdot 5}{7\cdot 2}}={\frac {5}{14}}$

Bibliografia

• Clara Bertinetto, Arja Metiäinen, Johannes Paasonen, Eija Voutilainen, Contaci!, Bologna, Zanichelli, 2013, ISBN 978.88.08.22009.7.

Collegamenti esterni

• Ubaldo Pernigo, Frazioni, ubimath.org. URL consultato il 20 maggio 2018.
• Matteo Ruffoni, Lezioni a scuola prima media, youtube.com. URL consultato il A.S. 2017-2018.
• Calcolatore di frazioni con passaggi: https://www.hackmath.net/en/calculator/fraction

Quiz

Punto aggiunto per ogni risposta corretta:
Punti sottratti per ogni risposta non corretta:
Ignora i coefficienti di domanda:

1 Il cameriere è entrato in sala con due litri e mezzo d'acqua in bottigliette da ${\frac {1}{4}}$, quante bottigliette sta portando questo abile cameriere?

	$10$
	$12$
	$9$
	$8$

2 Quale frazione è equivalente a ${\frac {3}{4}}$?

	${\frac {1}{2}}$
	${\frac {15}{20}}$
	${\frac {11}{25}}$
	${\frac {2}{3}}$

3 Nel negozio ci sono 16 bottiglie da ${\frac {1}{2}}$ di coca cola, a quanti litri corrispondono?

	$6+{\frac {3}{4}}$
	$8$
	$3$
	$13$

4 Sul tavolo c'è una torta divisa in quindici fette Luca ne mangia ${\frac {2}{15}}$, Quale frazione di torta rimane ?

	${\frac {13}{15}}$
	$6+{\frac {3}{15}}$
	$4$
	$9$

5 Qual è la frazione equivalente a ${\frac {3}{7}}$ ?

	${\frac {6}{14}}$
	${\frac {3}{11}}$
	${\frac {4}{8}}$
	${\frac {8}{16}}$

6 Qual è la frazione complementare a ${\frac {1}{7}}$ ?

	${\frac {7}{14}}$
	${\frac {6}{7}}$
	${\frac {7}{7}}$
	${\frac {5}{7}}$

7 Qual è la frazione complementare a ${\frac {5}{10}}$ ?

	${\frac {8}{17}}$
	${\frac {5}{10}}$
	${\frac {6}{8}}$
	${\frac {8}{9}}$

8 A casa di Lucia ci sono 8 bottiglie di succo di frutta da ${\frac {3}{4}}$ , Lucia ne prende 6 per portarle alla sua festa di compleanno. A quanti litri di succo di frutta corrispondono le 6 bottiglie?

	$4+{\frac {1}{2}}$
	$6+{\frac {1}{2}}$
	$4$
	$9$

9 Sul tavolo ci sono 6 bottiglie da ${\frac {3}{4}}$ di acqua, a quanti litri corrispondono?

	$4+{\frac {1}{2}}$
	$6+{\frac {1}{2}}$
	$4$
	$9$

10 Qual è la frazione complementare a ${\frac {3}{8}}$ ?

	${\frac {6}{16}}$
	${\frac {5}{8}}$
	${\frac {2}{8}}$
	${\frac {4}{8}}$

11 A quale frazione corrisponde il numero $0,4$ ?

	${\frac {4}{9}}$
	${\frac {40}{50}}$
	${\frac {2}{5}}$
	${\frac {4}{5}}$

12 Quanto fa 6 - ${\frac {6}{10}}$ ?

	${\frac {8}{17}}$
	$5{\frac {2}{5}}$
	${\frac {6}{8}}$
	${\frac {8}{9}}$

13 A quale frazione corrisponde il numero $0,06$ ?

	${\frac {6}{100}}$
	${\frac {6}{50}}$
	${\frac {12}{100}}$
	${\frac {3}{50}}$

14 un litro e mezzo di tè viene versato in nove tazze. Quale parte di litro ci sarà in ogni tazza,se in ognuna di esse si verseràla stessa quantità di tè ?</math>?

	${\frac {1}{2}}$
	${\frac {1}{6}}$
	${\frac {11}{25}}$
	${\frac {2}{3}}$

15 Giorgia ha speso i ${\frac {4}{10}}$ dei suoi soldi.Quanti soldi le rimangono ?

	${\frac {5}{10}}$
	${\frac {6}{10}}$
	${\frac {7}{13}}$
	${\frac {8}{20}}$