Angoli (scuola media)

Un angolo è la parte di piano^VK compresa tra due semirette^VK aventi l'origine^VK in comune.

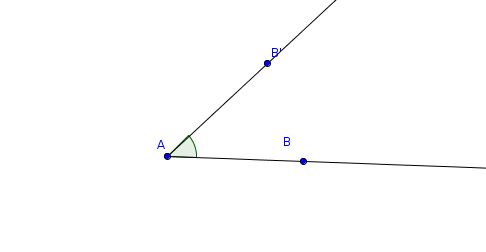
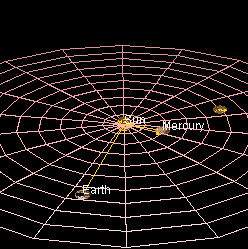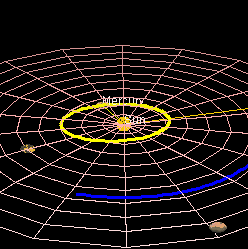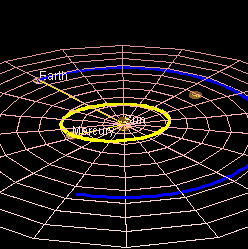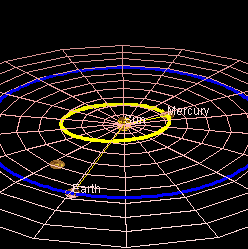
Una seconda definizione, più dinamica, associa l'angolo alla rotazione che una delle due semirette fa rispetto all'altra, un buon esempio è il movimento delle lancette dell'orologio ed anche il movimento dei pianeti in orbita o una qualsiasi rotazione. Nell'immagine qui sotto i raggi delle orbite della terra e di mercurio disegnano dinamicamente un angolo.

Mercuryorbitsolarsystem

Angolo convesso ed angolo concavo

Angolo concavo ed angolo convesso

Un angolo è detto convesso se non contiene i prolungamenti dei suoi lati, nella figura l'angolo $\alpha$ è convesso e l'angolo $\beta$ è concavo.

Angolo concavo ed angolo convesso

Aggiungendo i punti ${\text{B e D}}$ possiamo identificare gli angoli con le lettere latine maiuscole, l'angolo convesso è l'angolo ${\widehat {DAB}}$ mentre quello concavo è ${\widehat {BAD}}$, per convenzione gli angoli girano in senso antiorario.

Misura degli angoli

Vi sono due sistemi principali per misurare gli angoli nei quali come unità di misura si usano i gradi oppure i radianti.
Nella misura in gradi un angolo giro, immaginandoci le semirette come lancette di un orologio un giro completo, viene suddivisa in 360° gradi, nella seconda la misura dell'angolo corrisponde alla lunghezza dell'arco di circonferenza misurata in raggi.

Misura in gradi sessagesimali

Goniometro

Un angolo^VK misura un grado grado^VK se è la trecentosessantesima parte di un angolo giro, cioè di una rotazione completa.
I sottomultipli del grado seguono un sistema sessagesimale:

1° = 60', un grado corrisponde a 60 primi, 

e

1' = 60"  ed un primo corrisponde a 60 secondi.

La nostra misura del tempo si avvale dello steso sistema infatti 1 ora = 60 minuti e 1 minuto = 60 secondi.

Angoli noti

In base alla loro grandezza gli angoli vengono chiamati...

• 
  0°< Angolo acuto < 90°
• 
  Angolo retto = 90°
• 
  90°< Angolo ottuso < 180°
• 
  Angolo piatto = 180°
• 
  180°< Angolo concavo < 360°
• 
  Angolo giro = 360°

Misura in radianti

Nella figura seguente si mostra che la misura di una circonferenza di diametro 1 è $\pi$, numero che può essere conosciuto solo approssimativamente e che nei calcoli consideriamo uguale a 3,14.

Pi-unrolled-720

Considerando che il raggio è metà della circonferenza e pensando all'angolo come al percorso fatto in orbita per compiere un giro completo corrisponde a percorrere 3,14 diametri, o meglio 6,28 raggi, e quindi

$360^{\circ }=2\cdot \pi$

La misura di un angolo giro in radianti, cioè la misura della circonferenza misurata in raggi è proprio $\pi$.

Non è difficile comprendere che:

• $90^{\circ }={\frac {2\cdot \pi }{4}}={\frac {\pi }{2}}$
• $180^{\circ }={\frac {2\cdot \pi }{2}}=\pi$
• $270^{\circ }=3\cdot {\frac {\pi }{2}}={\frac {3}{2}}\pi$

In generale la misura di un angolo in radianti è un numero puro, cioè senza dimensioni che corrisponde al rapporto tra l'arco di circonferenza e il raggio

Radian measure

$\alpha ={\frac {arco}{raggio}}$

$1\ rad{\text{ corrisponde a }}57,296^{\circ }$

La misura di un angolo in radianti non dipende dalla circonferenza considerata infatti osservando la figura

The Economic Journal Volume 1 - p498

si comprende che all'aumento della lunghezza dell'arco corrisponde un aumento del raggio e quindi $\alpha ={\frac {Bb'}{Ab}}={\frac {Cc'}{Ac}}={\frac {Dd'}{Ad}}$

Le formule che permettono di passare dalla misura di un angolo in radianti $\alpha$ a quella in gradi $\alpha ^{\circ }$ e viceversa sono

${\frac {\alpha }{2\pi }}\cdot 360^{\circ }=\alpha ^{\circ }$

${\frac {\alpha ^{\circ }}{3}}60^{\circ }\cdot {2\pi }=\alpha$

Angoli noti in radianti

• 
  0< Angolo acuto < ${\frac {\pi }{2}}$
• 
  Angolo retto = ${\frac {\pi }{2}}$
• 
  ${\frac {\pi }{2}}$< Angolo ottuso < $\pi$
• 
  Angolo piatto = $\pi$
• 
  $\pi$< Angolo concavo < $2\pi$
• 
  Angolo giro = $2\pi$

Due rette tagliate da una trasversale

Angles between parallel lines and a transversal

A secondo delle posizioni che gli angoli assumono relativamente alle rette e gli uni nei confronti degli altri vengono denominati:

• gli angoli verdi sono una coppia di angoli alterni interni
• gli angoli gialli sono alterni esterni
• i blu e i rossi sono corrispondenti
• gli angoli rosa sono angoli coniugati interni
• gli angoli ocra sono coniugati esterni

Se le rette sono parallele:

• gli angoli alterni interni sono uguali tra loro
• gli alterni esterni sono uguali
• i corrispondenti sono uguali tra loro
• gli angoli coniugati sono supplementari, la loro somma fa 180°